[Interview] 면접 관련 정리14
트리 & 힙
- 트리 : 정점과 간선을 이용해 사이클을 이루지 않도록 구성한 Graph의 특수한 형태로, 계층이 있는 데이터를 표현하기에 적합하다.
- 힙 : 최댓값/최솟값을 찾아내는 연산을 쉽게 하기 위해 고안된 구조로, 각 노드의 키 값이 자식의 키 값보다 작지 않거나(최대힙) 그 자식의 키 값보다 크지 않은(최소힙) 완전이진트리.
힙 정렬(Heap Sort)
힙(heap)을 이용해 데이터를 정렬하는 방법으로, 병합 정렬과 퀵 정렬 만큼 빠르다.
힙(heap)은 최솟값이나 최댓값을 빠르게 찾아내기 위해 완전 이진 트리를 기반으로 하는 트리이다.
- 힙에는 최대힙과 최소힙이 존재하는데, 최대힙은 부모 노드가 자식 노드보다 큰 힙이다.
시간 복잡도는 모든 경우에서 O(nlogn)이다.
이진 트리 : 컴퓨터 안에서 데이터를 표현할 때, 데이터를 각 노드에 담은 뒤에 노드를 두 개씩 이어 붙이는 구조.
완전 이진 트리 : 데이터가 루트 노드 부터 시작해서 왼쪽 자식 노드, 오른쪽 자식 노드로 차근차근 들어가는 구조의 이진 트리.
static void heap_sort(int[] a, int size) { // size : a.length
// 원소가 1개 이하일 경우에는 정렬할 필요가 없다.
if(size < 2) {
return;
}
// 가장 마지막 요소의 부모 인덱스
int parentIdx = getParent(size - 1);
// max heap
for(int i = parentIdx; i >= 0; i--) {
heapify(a, i, size - 1);
}
for(int i = size - 1; i > 0; i--) {
// root인 0번째 idx와 i번째 idx 교환
// 0 ~ i-1 까지 max heap을 만족하도록 재구성
swap(a, 0, i);
heapify(a, 0, i-1);
}
}
// 부모 노드 = (자식 노드 - 1) / 2
static int getParent(int child) {
return (child - 1) / 2;
}
static void heapify(int[] a, int parentIdx, int lastIdx) {
// 부모 노드의 자식 노드 인덱스를 구한다.
// 왼쪽 자식 노드 = 부모 노드 X 2 + 1
// 오른쪽 자식 노드 = 부모 노드 X 2 + 2
int leftChildIdx = 2 * parentIdx + 1;
int rightChildIdx = 2 * parentIdx + 2;
int largestIdx = parentIdx;
/*
* leftChild node와 비교
* 자식 노드 인덱스가 트리의 크기를 넘지 않으면서, 현재 가장 큰 인덱스보다 더 클 경우
* largestIdx를 왼쪽 자식노드 인덱스로 바꾼다.
*/
if(leftChildIdx <= lastIdx && a[largestIdx] < a[leftChildIdx]) {
largestIdx = leftChildIdx;
}
if(rightChildIdx <= lastIdx && a[largestIdx] < a[rightChildIdx]) {
largestIdx = rightChildIdx;
}
/*
* largestIdx와 부모 노드가 같지 않다는 것은
* 비교 과정에서 현재 부모 노드보다 큰 노드가 존재했다는 의미이다.
* 그럴 경우, 해당 자식 노드와 부모 노드를 교환해주고,
* 교환된 자식 노드를 부모 노드로 삼은 서브트리를 검사하도록 재귀 호출.
*/
if(parentIdx != largestIdx) {
swap(a, largestIdx, parentIdx);
heapify(a, largestIdx, lastIdx);
}
}
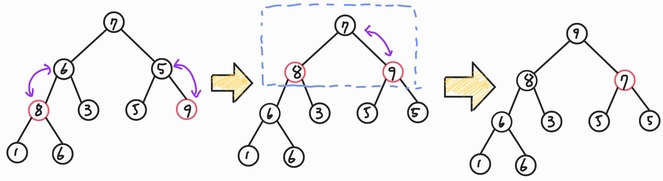
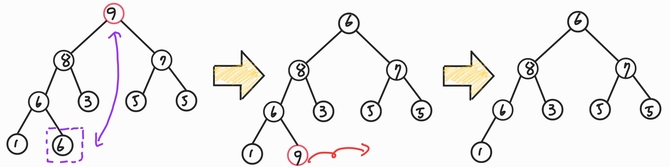
- 최대 힙으로 만든 뒤 최댓값을 추출하는 과정이다.
- 힙 정렬이 가장 유용한 경우는 전체 자료를 정렬하는 것이 아닌, 가장 큰 값 몇개만 필요할 때 처럼 최댓값, 최솟값을 뽑아낼 경우다.
계수 정렬(Counting Sort)
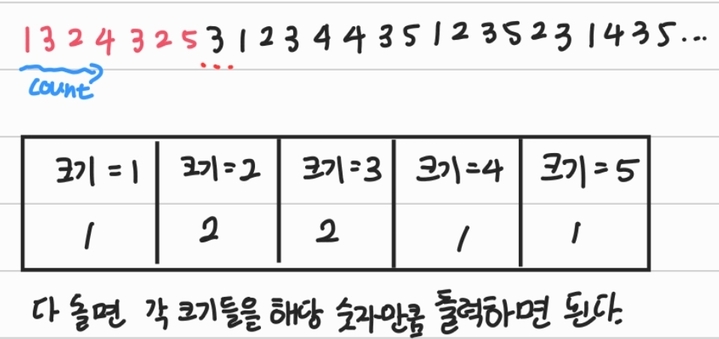
- 크기를 기준으로 개수를 세는 알고리즘이다.
- ‘범위 조건’이 있는 경우에 한에서 굉장히 빠른 알고리즘이다.
- Ex) 5이하의 자연수 데이터들을 오름 차순 정렬.
- 시간 복잡도 : O(n+k) (k는 배열에서 등장하는 최대값)
int count[k];
for(int i = 0; i < k; i++) {
count[i] = 0;
}
for(int i = 0; i < arr.length; i++) {
count[arr[i]-1]++;
}
for(int i = 0; i < k; i++) {
if(count[i] != 0) {
for(int j = 0; j < count[i]; j++) {
// print(i+1)
}
}
}
이분 탐색(Binary Search)
- 탐색 범위를 두 부분으로 분할하면서 찾는 방식
- 장점 : 처음부터 끝까지 돌면서 탐색하는 것(선형 탐색)보다 훨씬 빠르다.
- 단점 : 값이 정렬되어 있어야 한다.
// 배열에서 m값 찾기
static int binary_search(int[] arr, int m) {
Arrays.sort(arr); 값을 정렬하고 시작
int start = 0;
int end = arr.length - 1;
int mid = 0;
while(start <= end) {
mid = (start + end) / 2;
if(arr[mid] == m) {
return mid;
}else if(arr[mid] < m) {
start = mid + 1;
}else if(arr[mid] > m) {
end = mid - 1;
}
}
}
DFS & BFS
- 그래프를 탐색하는 방법에는 크게 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있다.
- 그래프를 탐색한다는 것은 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것이다.
DFS(Depth-First Search)
- 최대한 깊이 내려간 뒤, 더이상 갈 곳이 없을 경우 옆으로 이동
- 모든 경로를 방문해야 할 경우 적합하다.
- 스택, 재귀 함수를 통해 구현.
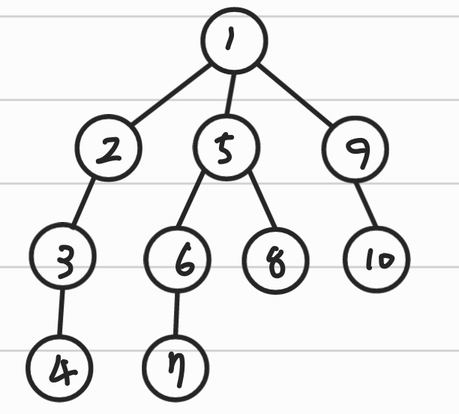
재귀 형태
static void dfs(int start) {
check[start] = true;
for(int node : arr[start]) {
if(!check[node]) {
dfs(node);
}
}
}
Stack 자료구조 사용
static Stack<Integer> stack = new Stack<>();
static void dfs() {
stack.push(1); // 시작 노드를 스택에 넣는다.
visited[1] = true; // 시작 노드 방문 처리
while(!stack.isEmpty()) {
int nodeIndex = stack.pop();
for(int node : arr[nodeIndex]) {
if(!visited[node]) {
stack.push(node);
visited[node] = true;
}
}
}
}
BFS(Breadth-First Search)
- 최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동
- 최소 비용(모든 곳을 탐색하는 것 보다 최소 비용이 우선일 경우)에 적합
- 큐를 통해 구현(해당 노드의 주변부터 탐색)
static Queue<Integer> q = new LinkedList<>();
static void bfs(int start) {
q.add(start);
check[start] = true;
while(!q.isEmpty()) {
start = q.poll();
for(int node : arr[start]) {
if(!check[node]) {
q.add(node);
check[node] = true;
}
}
}
}
댓글남기기